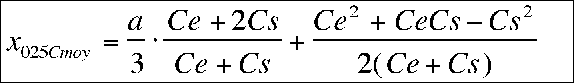How does a hang-glider fly?
Any profile of wing, under the effect of the air flow is subjected to a series of pressures and depressions whose resultant can break up into two forces:
- trainÈe which is opposed to the advance of the wing (not drawn on the diagram)
- the bearing pressure, much more interesting, which tends to make assemble the wing while being opposed to the weight of the model. It applies to the quarter of the mean wing chord.
The more one inclines the wing, the more the bearing pressure increases, but also more trainÈe increases.
These principles are valid for any profile of wing.
Finally it should be known that a profile advancing in the air tends to rock in a direction or the other (to pull up or prick) according to its particular characteristics. The swing is due to a couple whose moment can be either positive (tendency to pull up) or negative (tendency to prick). This moment is noted Cm0 in our catalogues of profiles.
A hang-glider does not have stabilizer. It uses either of the self-stabilizing profiles or a twist making the wing self-stabilizing. The self-stabilizing profiles are those which have one positive Cm0 moment.
The rotational movements of the wing are done around the centre of gravity of the model.
When the wing is correctly regulated, a balance is reached:
- the bearing pressure balances the weight of the model (Mg)
- the moment of the couple created by the bearing pressure around the centre of gravity balances the moment of the Cm0 profile
If, under the effect of a gust for example, the wing came to pull up, it would occur then what follows:

- if the wing pulls up, the bearing pressure increases,
- if the bearing pressure increases, the diving moment created by the bearing pressure compared to the centre of gravity increases and its moment (bearing pressure X outdistances CDG with C/4) is higher in absolute value than the Cm0 moment
== > the wing pricks, its bearing pressure decreases until reaching its initial value or all becomes again stable.
Thus, under the effect of a disturbance, a hang-glider returns to its position of balance. This is why it is said that it is self-stabilizing.
autostability by twist: formulate twist of Panknin
It is also possible to obtain a balance of the moments by introducing a twist of the wing calculated starting from the aerodynamic characteristics of the profiles of root and of salmon all the problem is to know to calculate the value of the twist...
With the authorization of the authors, I propose to you, in this paragraph, a translation of a page of the server http://www.halcyon.com/bsquared/Panknin.html based on work of Dr. Walter Panknin who allows to determine the geometrical twist to introduce when designing wing.
There are six variables which influence the velor of the twist:
tapering:
The more the wing is frayed, the more it will have to be twisted. This is due to the loss of effectiveness of the profile when the salmon cord becomes small.
lengthening:
The larger lengthening is, the less it is necessary to bore the wing. N the other hand, when lengthening increases, in proportion the cord decreases, and it becomes difficult to build a rigid wing in torsion...
the angle of flÍche:
The more there is flÍche, the less it is necessary to bore. However, beyond 20° of flÍche the air flow can be disturbed entrainant difficulties to control the flight...
coeeficients of moment of the profiles (Cm0):
The total moment of the wing must be positive to guarantee stability. Part of this moment is obtained by the couple to be pulled up from the control surfaces but it is also influenced by the moments in pitching of the profiles used. The contemporary hang-gliders out of arrow use for the pluspart profiles with Cm0 close to zero.
The static level of required stability:
To increase the static stability of the wing (by advancing the centre of gravity) forces to increase the twist of the wing.
The value of Cz of flight to the neutral:
The weaker selected Cz is, the less it is necessary to bore the wing. It east Èuivalent with trimmer to prick on a plane with stab to fly more quickly.
Angles of chock of the profiles with null bearing pressure (alpha0)
If one uses profiles of root and of salmon different or at least from which the alpha0 are different, the geometrical twist must be tiny room of the value of the difference of the 2 alpha0. It is interesting to choose a alpha0 salmon higher than the alpha0 of root
The formula of Panknin is the following one:
has total = [ (K1 · Cm0 empl + K2 · Cm0 saum ) - Cz · ms ] / [ 1,4.10 -5 · L 1,43 · G ]
has geo = geometrical angle of twist = has total - ( has 0 empl - has 0 saum )
with:
B = 1/2 scale
Cs = cord salmon
This = cord root
moyC = average of the cords = (Ce+Cs)/2
L = lengthening = 2b/moyC
EFF = tapering = Cs/Ce
G = angle of flÍche calculated to the 1/4 of the cord
K1 = 1/4 · (3 + 2.eff + EFF 2 )/(1 + EFF + EFF 2 )
K2 = 1 - K1
has 0 empl = angle with null bearing pressure for the profile of root
has 0 saum = angle with null bearing pressure for the salmon profile
Cm0 empl = coeff of moment for the profile of root
Cm0 saum = coeff of moment for the salmon profile
Cz = coeffecient of bearing pressure
ms = statitic margin (factor of stability)
If you have the spreadsheet microsoft Excel, all is included in the worksheet provided low...
You can also find with the address of the server bdquared mentioned above of the programs for QuickBASIC but with English units (inches, ounce and others...). One also finds there the references complete of the publications of Dr.. Panknin.
Lastly, for those which prefer to carry out calculations one line, you will find on the Rose site of the winds a page with Javascript which functions with wonder.
where to place the centre of gravity on a hang-glider?
Who didn't put this question?
The centre of gravity must imperatively be located between the
nose and the quarter of the mean aerodynamic chord. The quarter of
the mean aerodynamic chord is the point where applies the
resultant of the forces and moments aerodynamic. One finds of it
the definition theoretical low.
If the centre of gravity is placed behind the quarter of the
average aerodynamic cord, the wing is unstable and completely
impilotable... If the centre of gravity is too ahead, it is hardly
less serious, the wing " marsouine " by carrying out oscillations
around the axis of the pitching, oscillations which can, at worst
if the control surfaces are not sufisament dimensioned to be able
to increase the moment to pull up, not diminishing and leading to
the crash...
One can define a factor of stability (or strokes static) of a hang-glider like the relationship between the distance separating the centre of gravity from the quarter of the mean aerodynamic chord and the value of this mean aerodynamic chord.
Typically, a factor of stability of 5% (0,05) led to a healthy wing. The pilots more the men with a moustache will porront to go down in the neighbourhoods from 2%.
Even if the wing is calculated for 5%, it is advisable during the first flights to slightly advance the centre of gravity to obtain 10% of even if it means stability to slightly raise the control surfaces to compensate. Once the wing well in hands, one can then move back to obtain the behavior of its dreams...
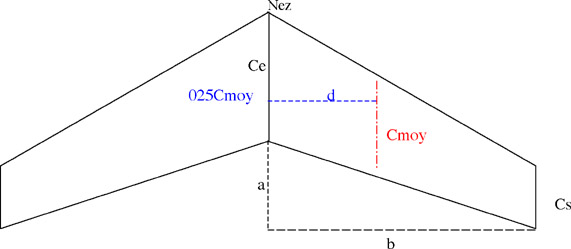
How to calculate the position of the average cord?
It is only one business of geometry. The following diagram represents a hang-glider " traditional " in delta with or without arrow.
you will find here a worksheet Excel allowing you to design a hang-glider with or without twist, to calculate the co-ordinates of the average cord with or without flÍche as well as the position of the centre of gravity. You will be able to even evaluate the order of magnitude the speed of flight of your wing, function of selected Cz and the estimated mass of the model (I said order of magnitude well!
theoretical equations:
For those which like the math and wish to check my calculations, the calculation of mean aerodynamic cord is based upon the following equations :
Lenght of mean aerodynamic cord is :
![]()
for our tapered wings :
C(y) = Ce + y.(Cs - Ce)/b ( equation (1))
while solving the integral gives :
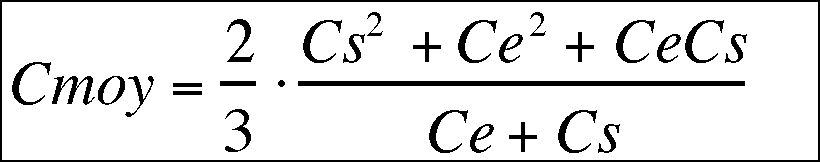
distance between root and mean cord is :
![]()
Finally, the most usefull is the distance between the nose and position of 1/4 of the mean cord :
![]()
It uses the parameter a which is the "hole" of the arrow :