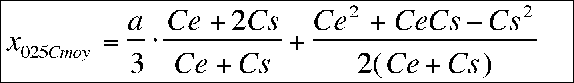Comment vole une aile volante ?
Tout profil d'aile, sous l'effet de l'écoulement de l'air est soumis à une série de pressions et depressions dont la résultante peut se décomposer en deux forces :
- la trainée qui s'oppose à l'avancement de l'aile (pas dessinée sur le schéma)
- la portance, beaucoup plus intéressante, qui tend à faire monter l'aile en s'opposant au poids du modèle. Elle s'applique au quart de la corde moyenne de l'aile.
Plus on incline l'aile, plus la portance augmente, mais aussi plus la trainée augmente.
Ces principes sont valables pour tout profil d'aile.
Enfin il faut savoir qu'un profil avançant dans l'air a tendance à basculer dans un sens ou dans l'autre (cabrer ou piquer) selon ses caractéristiques propres. Le basculement est dû à un couple dont le moment peut être soit positif (tendance à cabrer) soit négatif (tendance à piquer). Ce moment est noté Cm0 dans nos catalogues de profils.
Une aile volante ne dispose pas de stabilisateur. Elle utilise soit des profils autostables soit un vrillage rendant l'aile autostable. Le profils autostables sont ceux qui ont un moment Cm0 positif.
Les mouvements de rotation de l'aile se font autour du centre de gravité du modèle.
Lorsque l'aile est correctement réglée, un équilibre est atteint :
- la portance équilibre le poids du modèle (Mg)
- le moment du couple créé par la portance autour du centre de gravité équilibre le moment du profil Cm0
Si, sous l'effet d'une rafale par exemple, l'aile venait à cabrer, il se passerait alors ce qui suit :

- si l'aile cabre, la portance augmente,
- si la portance augmente, le couple à piquer créé par la portance par rapport au centre de gravité augmente et son moment (portance x distance CDG à C/4) est supérieur en valeur absolue au moment Cm0
==> l'aile pique, sa portance diminue jusqu'à atteindre sa valeur initiale ou tout redevient stable.
Donc, sous l'effet d'une perturbation, une aile volante revient à sa position d'équilibre. C'est pourquoi on dit qu'elle est autostable.
autostabilité par vrillage : formule de vrillage de Panknin
Il est également possible d'obtenir un équilibre des moments en introduisant un vrillage de l'aile calculé à partir des caractéristiques aérodynamiques des profils d'emplanture et de saumon. tout le problème est de savoir calculer la valeur du vrillage ...
Avec l'autorisation des auteurs, je vous propose, dans ce paragraphe, une traduction d'une page du serveur http://www.halcyon.com/bsquared/Panknin.html basée sur les travaux du Dr Walter Panknin qui permet de déterminer le vrillage géométrique à introduire lors de la conception d'une aile.
Il y a six variables qui influencent la veleur du vrillage :
l'effilement :
Plus l'aile est effilée, plus elle devra être vrillée. Ceci est dû à la perte d'efficacité du profil quand la corde de saumon devient petite.
l'allongement :
Plus l'allongement est grand, moins il faut vriller l'aile. En contrepartie, lorsque l'allongement augmente, en proportion la corde diminue, et il devient difficile de construire une aile rigide en torsion ...
l'angle de flêche :
Plus il y a de flêche, moins il faut vriller. Cependant, au delà de 20° de flêche l'écoulement de l'air peut être perturbé entrainant des difficultés pour contrôler le vol ...
les coeeficients de moment des profils (Cm0) :
Le moment global de l'aile doit être positif pour garantir la stabilité. Une partie de ce moment est obtenue par le couple à cabrer issu des gouvernes mais il est également influencé par les moments en tangage des profils utilisés. Les ailes volantes contemporaines en flèche utilisent pour la pluspart des profils à Cm0 proches de zéro.
Le niveau de stabilité statique requis :
Augmenter la stabilité statique de l'aile (en avançant le centre de gravité) impose d'augmenter le vrillage de l'aile.
La valeur du Cz de vol au neutre :
Plus le Cz choisi est faible, moins il est nécessaire de vriller l'aile. C'est éuivalent à trimmer à piquer sur un avion avec stab pour voler plus vite.
Les angles de calage des profils à portance nulle (alpha0)
Si l'on utilise des profils d'emplanture et de saumon différents ou du moins dont les alpha0 sont différents, le vrillage géométrique devra être réduit de la valeur de la différence des 2 alpha0. Il est intéressant de choisir un alpha0 de saumon supérieur à l'alpha0 d'emplanture
La formule de Panknin est la suivante :
atotal = [(K1· Cm0empl + K2· Cm0saum ) - Cz·ms] / [ 1,4.10-5 · l 1,43 · g ]
ageo = angle de vrillage géométrique = atotal - (a0empl - a0saum)
avec :
b = 1/2 envergure
Cs = corde saumon
Ce = corde emplanture
moyC = moyenne des cordes = (Ce+Cs)/2
l = allongement = 2b/moyC
eff = effilement = Cs/Ce
g = angle de flêche calculé au 1/4 de la corde
K1 = 1/4 · (3 + 2.eff + eff2)/(1 + eff + eff2)
K2 = 1 - K1
a0empl = angle à portance nulle pour le profil d'emplanture
a0saum = angle à portance nulle pour le profil de saumon
Cm0empl = coeff de moment pour le profil d'emplanture
Cm0saum = coeff de moment pour le profil de saumon
Cz = coeffecient de portance
ms = marge statitique (facteur de stabilité)
Si vous disposez du tableur microsoft Excel, tout est repris dans la feuille de calcul fournie plus bas ...
Vous pouvez également trouver à l'adresse du serveur bdquared mentionnée plus haut des programmes pour QuickBASIC mais avec des unités Anglaises (inches, ounce et autres ...). On y trouve également les références complètes des publications du Dr. Panknin.
Enfin, pour ceux qui préfèrent effectuer les calculs on line, vous trouverez sur le site Rose des vents une page avec du javascript qui fonctionne à merveille.
où placer le centre de gravité sur une aile volante ?
Qui ne s'est pas posé cette question ?
Le centre de gravité doit impérativement
être situé entre le nez et le quart de la corde
aérodynamique moyenne. Le quart de la corde
aérodynamique moyenne est le point où s'applique la
résultante des forces et moments aérodynamiques. On
en trouve la définition théorique plus bas.
Si le centre de gravité est placé derrière le
quart de la corde aerodynamique moyenne, l'aile est instable et
totalement impilotable... Si le centre de gravité est trop
en avant, c'est à peine moins grave, l'aile "marsouine" en
effectuant des oscillations autour de l'axe de tangage,
oscillations qui peuvent, au pire si les gouvernes ne sont pas
sufisament dimensionnées pour pouvoir augmenter le moment
à cabrer, ne pas s'amortir et conduire au crash ...
On peut définir un coefficient de stabilité (ou marge statique) d'une aile volante comme le rapport entre la distance séparant le centre de gravité du quart de la corde aérodynamique moyenne et la valeur de cette corde aérodynamique moyenne.
Typiquement, un coefficient de stabilité de 5% (0,05) conduit à une aile saine. Les pilotes les plus moustachus porront descendre aux alentours de 2%.
Même si l'aile est calculée pour 5%, il sera prudent lors des premiers vols d'avancer légèrement le centre de gravité pour obtenir 10% de stabilité quitte à relever légèrement les gouvernes pour compenser. Une fois l'aile bien en mains, on peut alors reculer pour obtenir le comportement de ses rêves...
Comment calculer la position de la corde moyenne ?
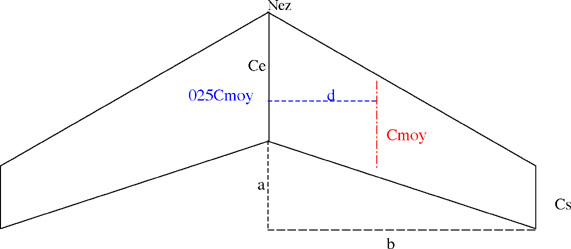
Ce n'est qu'une affaire de géométrie. Le schéma suivant représente une aile volante "classique" en delta avec ou sans flèche.
vous trouverez ici une feuille de calcul excel vous permettant de concevoir une aile volante avec ou sans vrillage, calculer les coordonnées de la corde moyenne avec ou sans flêche ainsi que la position du centre de gravité. Vous pourrez même évaluer l'ordre de grandeur de la vitesse de vol de votre aile, fonction du Cz choisi et de la masse estimée du modèle (j'ai bien dit ordre de grandeur ! ...)
les équations théoriques :
Pour ceux qui aiment les maths et souhaitent vérifier mes calculs, le calcul de la corde aérodynamique moyenne est basé sur les quelques équations suivantes :
La longueur de la corde aérodynamique moyenne se calcule par une belle intégrale :
![]()
avec pour nos ailes trapézoïdales :
![]() (équation (1))
(équation (1))
On obtient en résolvant l'intégrale :
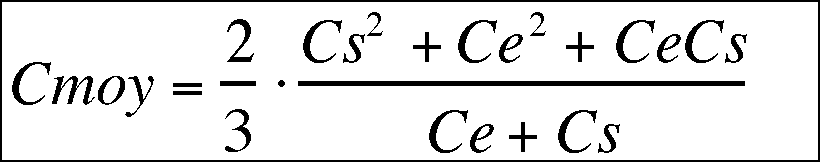
la distance entre l'emplanture et la corde moyenne se calcule à l'aide de (1) et vaut :
![]()
Enfin, le plus utile est la distance entre le nez et la position du point "quart de la corde moyenne".
![]()
Soit en faisant intervenir le paramètre "creux de la flèche" que j'ai noté "a".